Siteswap List
- This is an attempt to structure basic siteswap patterns (no derivations). Of course you can throw stuff like: „5648323945AFF955“ (which is quite fun) but my aim here is to find out the inherent basic patterns on which the most commonly used siteswaps are build
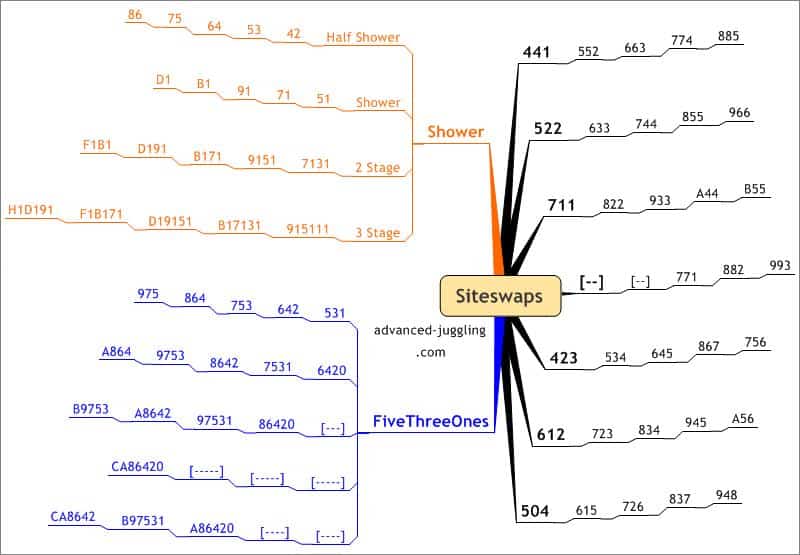
- You can easily see in some of the rows (like in the 531´s) that by adding or subtracting to the base you can figure out the pattern with four or five…. balls. So you get 531 -> 642 -> 753.
- Amazing! for me since i´m not a mathematician. It took me a long time until i understood that 534 with four balls is in some ways similar to 645 with five balls.
Just click each siteswap to view the trick with JugglingLab Simulator
| Asynchronus | 3 | 4 | 5 | 6 | 7 |
? | 423–> | 534–> | 645–> | 756 –> | 867 |
| Half shower | 42 | 53 | 64 | 75 | 86 |
| Shower | 51 | 71 | 91 | B1 | D1 |
| High Low Shower | 7131 | 9151 | B171 | D191 | |
| 3 Stage | 915111 | B17131 | D19151 | ||
1Stage | 3 | 4 | 5 | 6 | 7 |
2 Stage | 42 | 53 | 64 | 75 | 86 |
Five Three Ones | 531 | 642 | 753 | 864 | 975 |
4 Stage | 6420 | 7531 | 8642 | 9753 | A864 |
5 Stage | 86420 | 97531 | A8642 | B9753 | |
6 Stage | A86420 | B97531 | CA8642 | ||
7Stage | CA86420 | DB97531 | |||
| Unsorted | 3 | 4 | 5 | 6 | 7 |
| 504 | 615 | 726 | 837 | 948 | |
| 711 | 822 | 933 | A44 | B55 | |
| 522 | 633 | 744 | 855 | 966 | |
| 441 | 552 | 663 | 774 | 885 | |
| 64203 | 714 | 66661 | |||
| 63123 | 741 | 771 | |||
| 50505 | 80 | 7733 | |||
| 8040 | 5551 | 75751 | |||
| 52535 | 88441 | ||||
| 773 | |||||
| Synchronous | 3 | 4 | 5 | 6 | 7 |
| High-Low´s | (4x,2)(2,4x) | (6,4x)(2x,4) (4x,6)(4,2x) | (6x,4)(4,6x) | (8,6x)(4x,6) (6x,8)(6,4x) | (8x,6)(6,8x) |
| (2x,4)(4,2x) | (6x,4)(2,4x) (4,6x)(4x,2) | (6,4x)(4x,6) | (8x,6)(4,6x) (6,8x)(6x,4) | (8,6x)(6x,8) | |
| Half shower | (6,2)(2,6) | (8,4)(4,8) | |||
| (6x,2x)(2x,6x) | (8x,4x)(4x,8x) | ||||
| Shower | (4x,2x) | (6x,2x) | (8x,4x) |
Just another idea :
I would be glad to receive E-Mails with your suggestions
1 Kommentar. Hinterlasse eine Antwort
[…] the full List of Siteswaps […]